Як знайти діагональ трапеції?

Перш, ніж розбиратися, як знайти діагональтрапеції, згадаємо, що таке трапеція. У планіметрії трапецією називають чотирикутник, у якого дві протилежні сторони паралельні один одному. Ці паралельні сторони називають підставами трапеції, а решта - бічними сторонами. Бічні сторони можуть бути однаковими, тоді ми маємо справу з рівнобедреної трапецією.

Далі детально розберемо порядок знаходження довжинидіагоналей для загального випадку - неравнобедренной трапеції. При цьому будемо виходити з того, що вихідними даними є довжини всіх чотирьох сторін трапеції, кути біля основи невідомі.

Розрахунок діагоналі трапеції

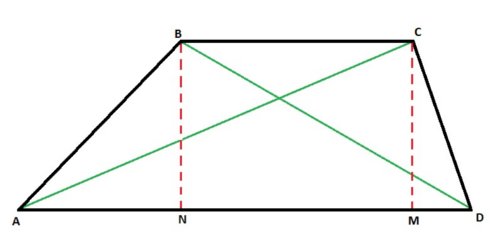
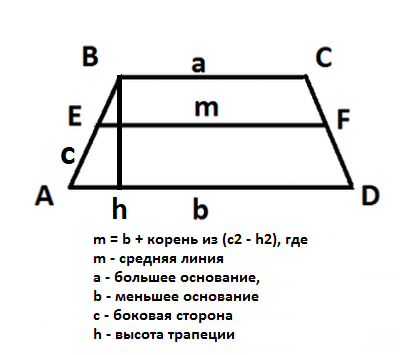
У зображеної на малюнку трапеції ABCD є дві діагоналі AC і BD. Порядок перебування їх довжини однаковий, тому розглянемо все на прикладі знаходження діагоналі BD, противолежащей ˂BAD.

Діагональ BD одночасно є стороною трикутника ABD і може бути розрахована по теоремі косинусів за допомогою формули:

BD = √ (AB²+ AD²-2AB^.AD^.cos ˂BAD)

У цій формулі нам відомі всі величини, крімкосинуса ˂BAD. Щоб обчислити його, нам необхідно буде виконати невелике перетворення малюнка. «Виріжемо» з вихідної трапеції прямокутник BNMC. В результаті отримаємо трикутник ABD ", в якому сторона BD" буде дорівнює стороні трапеції CD.

˂BAD "в трикутнику дорівнює ˂BAD в трапеції, такяк ніяких перетворень з трикутником ABN ми не виконували. Отже, в цьому трикутнику ABD "сторона AB нам відома, сторона BD" = CD, а сторона AD "= AD - NM = AD - BC.

Виходить, що за теоремою косинусів cos ˂BAD = cos ˂BAD "= (AB² + AD "² - BD "²) / 2AB^.AD "= (AB² + (AD - BC)² - CD²) / 2AB^.(AD - BC)

Підставивши тепер отриманий вираз в знайдену раніше формулу, отримаємо:

BD = √ (AB²+ AD²-2AB^.AD^.cos ˂BAD) = √ (AB²+ AD²-2AB^.AD^.(AB² + (AD - BC)² - CD²) / 2AB^.(AD - BC)) = √ (AB² + AD² - AD^.(AB² + (AD - BC)² - CD²) / (AD - BC)) = √ (AB² + AD² - AD^.(AD - BC)²/ (AD - BC) - AD^.(AB² - CD²) / (AD - BC)) = √ (AB² + AD² - AD² + AD^.BC - AD^.(AB² - CD²) / (AD - BC)) = √ (AB² + AD^.BC - AD^.(AB² - CD²) / (AD - BC))

BD = √ (AB² + AD^.BC - AD^.(AB² - CD²) / (AD - BC))

Отримана формула діагоналі трапеції справедлива для будь-яких значень довжин сторін вихідного чотирикутника.

Для другої діагоналі формула відповідно набуде вигляду:

AC = √ (CD² + AD^.BC - AD^.(CD² - AB²) / (AD - BC))

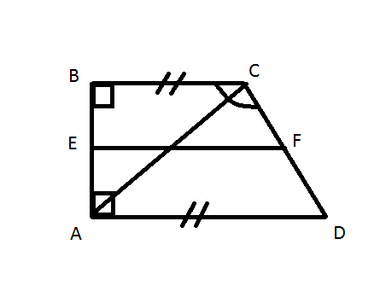
Діагональ рівнобедреної трапеції

Якщо вас цікавить, як знайти діагональ рівнобедреної трапеції, отриману формулу можна значно спростити. Адже в рівнобедреної трапеції AB = CD, отже AB² - CD² = 0 і формула довжини діагоналі приводиться до вигляду:

BD = √ (AB² + AD^.BC)

Діагоналі рівнобедреної трапеції дорівнюють один одному, тому друга діагональ знаходиться за тією ж формулою.

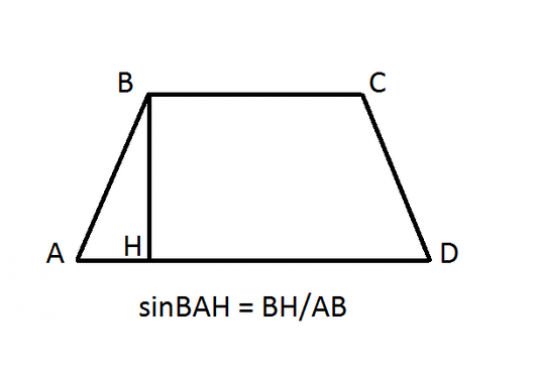
У тому випадку, якщо вихідними даними єдовжини підстав трапеції, одна з бічних сторін і кути при підставі, то задача знаходження діагоналі трапеції зводиться до розрахунку сторони трикутника по теоремі косинусів.