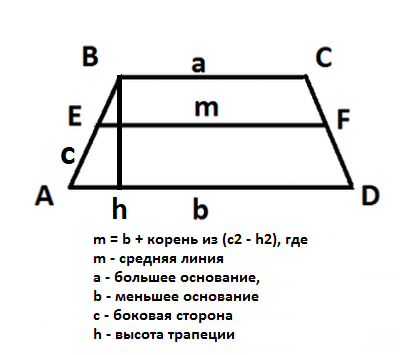
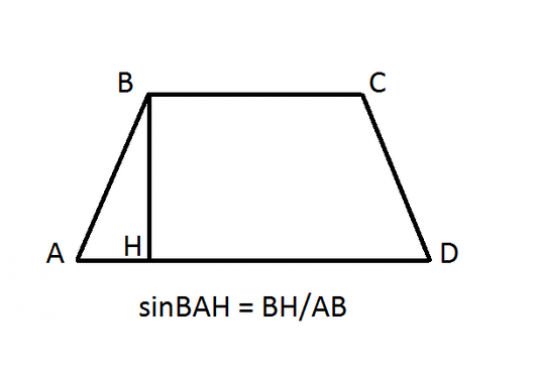
Як знайти середню лінію трапеції?

Відрізок прямої, яка з'єднує середини бічнихсторін трапеції, називається середньою лінією трапеції. Про те, як знайти середню лінію трапеції і як вона співвідноситься з іншими елементами цієї фігури, ми розповімо нижче.
Теорема про середній лінії
Намалюємо трапецію, в якій AD - більшепідставу, BC - менше підставу, EF - середня лінія. Продовжимо підставу AD за точку D. Проведемо лінію BF і продовжимо її до перетину з продовженням підстави AD в точці О. Розглянемо трикутники ΔBCF і ΔDFO. Кути ∟BCF = ∟DFO як вертикальні. CF = DF, ∟BCF = ∟FDО, тому що ВС // АТ. Отже, трикутники ΔBCF = ΔDFO. Звідси боку BF = FO.
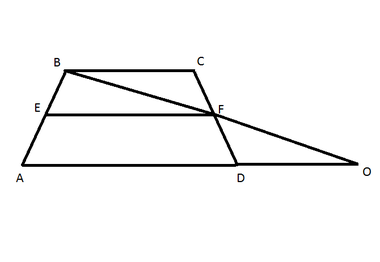
Тепер розглянемо ΔАВО і ΔEBF. ∟ABO загальний для обох трикутників. BE / AB = ½ за умовою, BF / BO = ½, оскільки ΔBCF = ΔDFO. Отже, трикутники ABO і EFB подібні. Звідси ставлення сторін EF / AO = ½, як і ставлення інших сторін.
Знаходимо EF = ½ AO. За кресленням видно, що AO = AD + DO. DO = BC як сторони рівних трикутників, значить, AO = AD + BC. Звідси EF = ½ АТ = ½ (AD + BC). Тобто довжина середньої лінії трапеції дорівнює напівсумі підстав.
Чи завжди середня лінія трапеції дорівнює напівсумі підстав?
Припустимо, що існує такий окремий випадок,коли EF ≠ ½ (AD + BC). Тоді ВС ≠ DO, отже, ΔBCF ≠ ΔDCF. Але це неможливо, оскільки у них рівні два кута і сторони між ними. Отже, теорема вірна при будь-яких умовах.
Завдання про середньої лінії
Припустимо, в нашій трапеції АВСD АD // ВС, ∟A = 90 °, ∟С = 135 °, АВ = 2 см, діагональ АС перпендикулярна боці. Знайдіть середню лінію трапеції EF.
Якщо ∟А = 90 °, то і ∟В = 90 °, значить, ΔАВС прямокутний.
∟BCA = ∟BCD - ∟ACD. ∟ACD = 90 ° за умовою, отже, ∟BCA = ∟BCD - ∟ACD = 135 ° - 90 ° = 45 °.
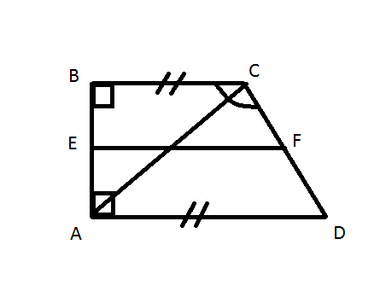
Якщо в прямокутному трикутнику ΔАВС один кут дорівнює 45 °, значить, катети в ньому рівні: АВ = ВС = 2 см.
Гіпотенуза АС = √ (АВ² + ВС²) = √8 см.
Розглянемо ΔACD. ∟ACD = 90 ° за умовою. ∟CAD = ∟BCA = 45 ° як кути, утворені січною паралельних підстав трапеції. Отже, катети AC = CD = √8.
Гіпотенуза AD = √ (AC² + CD²) = √ (8 + 8) = √16 = 4 см.
Середня лінія трапеції EF = ½ (AD + BC) = ½ (2 + 4) = 3 см.