Як знайти площу паралелепіпеда?

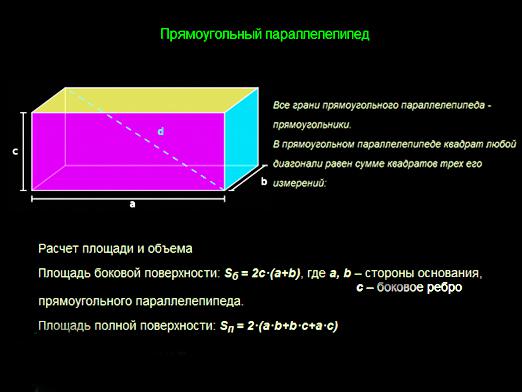
У геометричній фігурі паралелепіпед єшість граней - чотири основні і два підстави (за визначенням вони все є паралелограма). Якщо всі шість є прямокутниками, то паралелепіпед буде прямим. Грані знаходяться на протилежних сторонах рівні, при цьому вони паралельні. Чотири діагоналі паралелепіпеда сходяться в єдиній точці і діляться надвоє.

Щоб з'ясувати, як знайти площупаралелепіпеда, необхідно обчислити спершу площа всіх його підстав (позначається літерою - a), його збоку (позначається літерою - b), при цьому визначити, чому дорівнює довжина підстави і ребро.

Спершу проведемо висоту паралелограма (позначаємо буквою - h), потім ребро паралелепіпеда (позначаємо буквою - H). Або через довжини сторін (a, b, c).

Загальна площа підстав дорівнює: S = 2a * h або S = 2ac

Так як бічні грані - це прямокутники, то їх площа дорівнює: S = 2a * H і S = 2b * h або S = 2a * b, S = 2b * c

Отже, ми з'ясували, як знайти площупрямокутного паралелепіпеда - остаточна формула розрахунку пишеться так: S = 2ah + 2aH + 2bH = 2 (ah + aH + bH) або S = 2 (Sa + Sb + Sc) = 2 (ab + bc + ac), а саме, подвоєна сума площ граней паралелепіпеда.

Бувають випадки, коли бічні граніпаралелограма лежать під будь-яким кутом до його основи, тоді паралелепіпед є похилим. Тоді площа його бічних граней обчислюємо, знаючи їх висоту. При цьому площа підстав розраховується однаково.

Нічого складного.