Як знайти діагональ паралелограма?

Паралелограм є геометричноюфігуру, характерною особливістю якої є те, що у неї протилежні сторони паралельні і попарно рівні, а також діагоналі в ній перетинаються, і точка заходу ділить їх навпіл. Квадрат, ромб і прямокутник є паралелограма.

Діагональ паралелограма

Розглянемо, як знайти діагональ паралелограма. У параллелограмме:

Сума кутів, які прилягають до однієї сторони, завжди буде становити 180 градусів;
Точка, в якій діагоналі перетинаються, є центр симетрії паралелограма.
У будь-якому чотирикутнику, в тому числі в параллелограмме сума всіх кутів дорівнює 360 градусів;
Подвоєна сума квадратів двох суміжних сторін паралелограма завжди дорівнює сумі квадратів діагоналей.

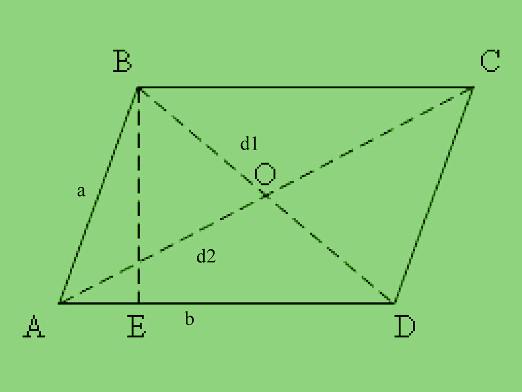
Для того щоб знати, як знайти велику діагональпаралелограма, треба визначитися з літерним позначенням. Наприклад, ми маємо паралелограм зі сторонами АВ і ВС. Маленькою літерою «а» позначимо одну довжину паралелограма, а маленькою літерою «в» буде друга його довжина. Маленькими літерами d1 d2 позначимо діагоналі. Для того щоб знайти діагональ паралелограма треба:

Значення властивостей паралелограма допомагає знайтипотрібне рішення. Діагоналі, які в точці заходу діляться навпіл, називаються биссектрисами. Менша бісектриса - для тупих кутів, велика для гострих кутів. Таким чином, коли розглядаються пари трикутників, одержуваних з однієї діагоналі і двох суміжних сторін геометричної фігури, інша половина діагоналі є ще і медіаною.
Трикутники, які виходять в результатіосвіти половинами діагоналі і паралельними сторонами будь-якого паралелограма вважаються подібними, також діагональ ділить таку геометричну фігуру на два трикутника, вони симетричні щодо заснування та абсолютно однакові.
Для знаходження великої діагоналі паралелограманеобхідно скористатися загальноприйнятою формулою, яка говорить про співвідношення суми квадратів довжин сторін, яка подвоюється і суми квадратів двох діагоналей. Формула буде мати такий вигляд: d1² + d2² = 2х (a² + b²).
Якщо велика діагональ - d2, тоді формула буде мати такий вигляд: d2 = {2х (a² + b²) - d1²}.

Розглянемо на прикладі, як знайти довжину діагоналіпаралелограма. Припустимо, що паралелограм має довжину сторін: а = 3, в = 8. Необхідно знайти ту діагональ, яка є більшою, при цьому буде відомо, що вона більше меншою на три см. Діагональ. Спочатку записуємо формулу в загальному вигляді, вона буде мати вигляд: d1² + d2² = 2 х (9 + 64) = 146, далі висловлюємо довжину меншої діагоналі: d1 = d2 - 3, підставивши то вираз в першу формулу, отримаємо: (d2 - 3) ² + d2² = 146

Зводимо в квадрат значення в дужках, отримуємо: d2² - 6х d2 + 9 + d2² = 14, 2х d2² - 6х d2 -135 = 0
Отримане квадратне рівняння вирішується, використовуючи дискриминант. Таким чином, діагональ дорівнює 9,85 і вона є позитивною величиною.